GENERATIONS SUR LES FORCES

1. NOTION DE FORCE

I-1.  Interaction entre objets

Exemple 1

Dans un match de football, pour jouer un corner, un joueur A pose le ballon sur le point de corner, prend son élan, tire et envoie le ballon à la surface de but adverse. Pour marquer le but, un attaquant B saute et dévie le ballon de la tête vers les buts. Le gardien s’élance du bon côté et stoppe le ballon.

Nous dirons que : 

• le ballon a été mis en mouvement par le joueur A (action du pied du joueur A sur le ballon) ;
• le mouvement initial du ballon a été modifié par le joueur B (action de la tête du joueur B sur le ballon) ;
• le ballon a été arrêté par le gardien (action des mains du gardien sur le ballon).

Exemple 2

Approchons un aimant d’une bille en acier immobile sur un plan horizontal : 

vient se coller à l’aimant.

La bille est mise en mouvement par l’action du de l’aimant.

Exemple 3

La bille et l’aimant précédents sont utilisés dans le dispositif ci-contre :

La bille est lâchée à partir du point A sur le plan incliné.

En l’absence de l’aimant, la bille décrit un segment de droite 

et atterrit en B.

En présence de l’aimant, la trajectoire de la bille est modifiée.

L’action de l’aimant modifie la présence de la bille.

Exemple 4 :

A l’extrémité inférieure d’un ressort dont l’autre extrémité 

est fixée, accrochons un solide (S) : le ressort s’allonge.

Le ressort se déforme sous l’action du solide (S). Le ressort s’allonge

Le ressort se déforme sous l’action du solide (S)

I-2. Définitions

On appelle force toute action capable :

• de produire le mouvement d’un corps ;
• ou de modifier le mouvement d’un corps ;
• ou de provoquer la déformation d’un corps.

On distingue l’action de contact et l’action à distance.

• Il y a interaction de contact (force de contact) lorsque le corps qui exerce l’action et le corps qui la subit sont en contact direct.

C’est le cas de l’exemple 1 entre le pied et le ballon, entre la tête et le ballon, entre les mains du gardien et le ballon ; c’est aussi le cas de l’exemple 4 entre le ressort et le solide (S).

• Il y a interaction à distance (force à distance) lorsque les deux corps qui interagissent n’ont pas besoin de se toucher.

C’est le cas des exemples 2 et 3 entre l’aimant et la bille.

Système    

On appelle système matériel (S), tout solide ou ensemble de solides que l’on se propose d’étudier. Tout ce qui n’appartient pas au système (S) constitue le milieu extérieur.

Force extérieure- force intérieure

Toute force exercée par le milieu extérieur sur le système est appelée force extérieure. Toute force exercée par une partie du système sur une autre partie du système est appelée force intérieure.

Exemple

Un camion (C) tire une remorque (R) par l’intermédiaire d’un câble.

• Si nous considérons le système constitué par la remorque, la force exercée par le camion sur la remorque est une force extérieure.
• Si nous considérons le système formé par le camion et la remorque, la force exercée par le camion sur la remorque est une force intérieure.

I-3. Effets d’une force

Une force se manifeste par ses effets : dynamique ou statique.

• Une force a un effet dynamique lorsqu’elle provoque ou modifie le mouvement d’un objet (exemples 1, 2 et 3) ;
• Une force a un effet statique lorsqu’elle modifie la forme d’un objet (exemple 4), ou lorsqu’elle contribue au maintien de l’équilibre, c'est-à-dire l’immobilité, du corps sur lequel elle s’exerce.

I-4. Représentation et caractéristiques d’une force

Exemple : Une personne tire sur un chariot par l’intermédiaire d’un câble.   

L’action mécanique exercée par l’opérateur sur le charriot a lieu suivant une direction et un sens bien déterminés.

Pour marquer cette direction et ce sens, on représente la force par un vecteur () : une force est une grandeur vectorielle.

Toute force est caractérisée par :

• un point d’application (origine du vecteur) : c’est le point où l’action s’exerce sur le corps considéré ;    
• une direction : c’est la droite suivant laquelle l’action s’exerce ;
• un sens : c’est sur la direction, le sens vers le quel l’action s’exerce ;
• une norme (ou module) : c’est l’intensité du vecteur force notée : .

Mesure de forces

La valeur d’une force se mesure avec un appareil appelé dynamomètre.

Dans le système international d’unités (S.I.), l’intensité d’une force s’exprime en newton (N).

Force motrice – Force résistante

Lorsqu’un solide est en mouvement, toute force qui favorise le mouvement est dite force motrice, toute force qui s’oppose au mouvement est dite force résistante.

Force localisée - Force répartie

Une force est dite localisée s’il existe un point d’application précis. Exemple : la force exercée par le câble sur le chariot.

Parfois les actions se répartissent sur toute une surface ou dans tout un volume ; la force est alors dite répartie. 

Exemple : Force exercée par l’air sur la voile d’un parachutiste.(voir figure)

Autres exemples : force de pression exercée par l’air sur les parois d’un ballon que l’on gonfle, force de pression exercée par un liquide sur les parois du liquide qui le contient.

2. EXEMPLES DE FORCES 

II-1. Tension d’un fil (ou d’un câble)

Dans l’exemple ci-dessus, l’opérateur déplace le charriot par l’intermédiaire du câble qui agit directement sur le charriot : on dit que le câble exerce une force appelée  tension du câble sur le charriot.

Généralement, la tension d’un fil (ou d’un câble est) notée .

II-2. Tension d’un ressort

Lorsqu’on exerce la force pour déformer le ressort, ce dernier exerce une force appelée tension du ressort pour s’opposer à sa déformation.

La tension tend à ramener le ressort dans sa position initiale : on dit que c’est une force de rappel.

La différence de longueur _x=l-loest appelé allongement du ressort. 

L’intensité de la tension d’un ressort est proportionnelle à l’allongement du ressort : 

Le coefficient de proportionnalité est appelé constante de raideur du ressort. Elle caractérise l’aptitude du ressort à s’opposer à toute déformation.

Unité : _T=kx, donc _k=T/x. _ks’exprime en newton par mètre _(N/m).

II-3. Réaction d’un support

Un solide placé sur un support est soumis de la part de ce dernier d’une force appelée réaction du support, souvent noté .

II-3-1. Cas d’un contact sans frottement (support lisse ou lubrifié ou sur coussin d’air)

Dans le cas d’un contact sans frottement, la réaction est toujours normale au support.

III-3-2. Cas d’un contact avec frottement (support rugueux)

’un contact avec frottement, la réaction du support a deux composantes :

• Une composante normale : la réaction normale  (réaction à l’enfoncement) ;
• une composante tangentielle : la réaction tangentielle 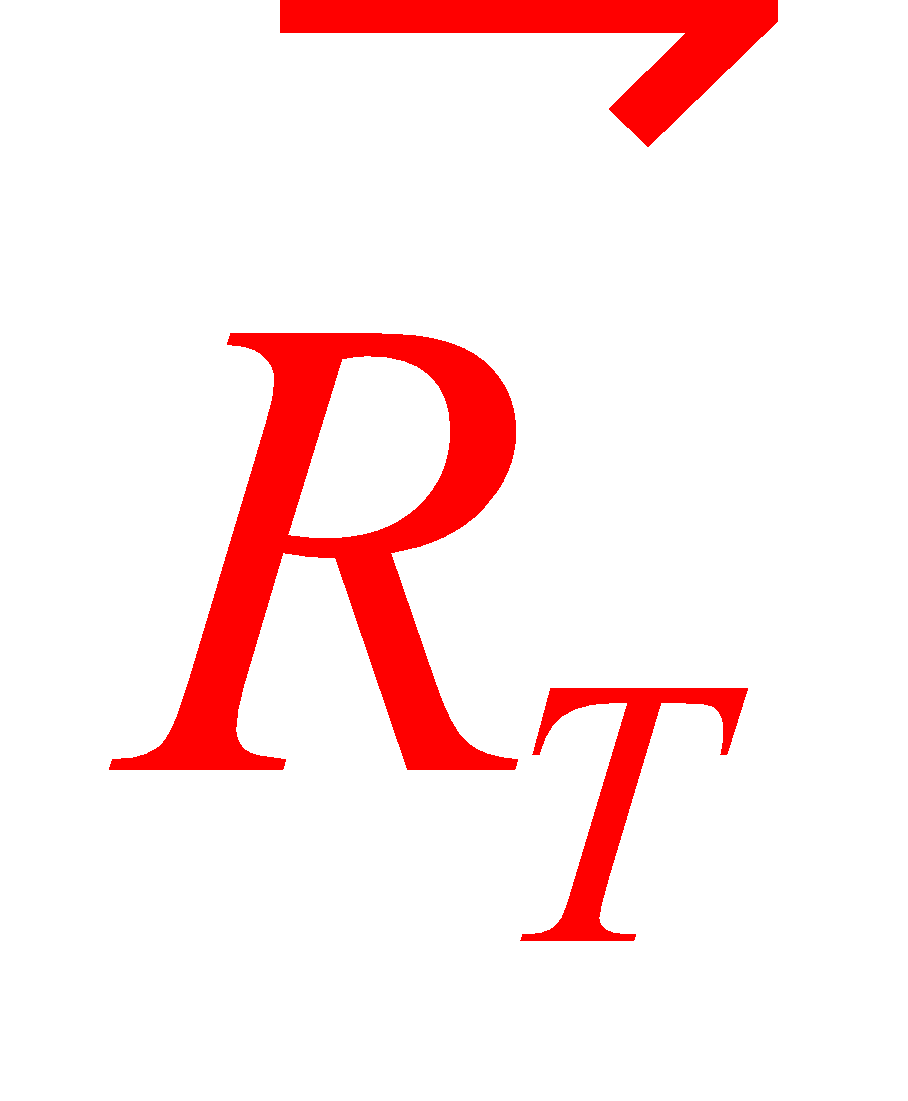souvent appelée force de frottement et notée .

La réaction globale du support sur le solide est la résultante des deux composantes :

 

 

 

 

 

 

II-4. La poussée d’Archimède

Lorsque qu’un corps est immergé dans un fluide, il subit de la part du fluide des forces pressantes qui s’exercent en chaque point du solide. Celles-ci sont perpendiculaires aux surfaces de contact entre le fluide et le solide et dirigées vers lui.

La poussée d’Archimède est la résultante de ces forces qui n’est donc pas nulle. 

Elle a les caractéristiques suivantes :

• Son point d’application est le centre de gravité du volume du solide immergé (le solide n’est pas forcément entièrement immergé).
• Sa direction est verticale.
• Son sens est vers le haut.
• Sa valeur est égale au poids du volume du solide immergé :

La poussée d’Archimède exercée par l’air sur le solide (l’air est un fluide) sera généralement négligée.

3. LE PRINCIPE DES INTERACTIONS (3^ème LOI DE NEWTON)

III-1. Enoncé 

Lorsqu’un corps (A) exerce sur un corps (B) une force (action), le corps (B) exerce, au même instant, sur le corps (A) une force 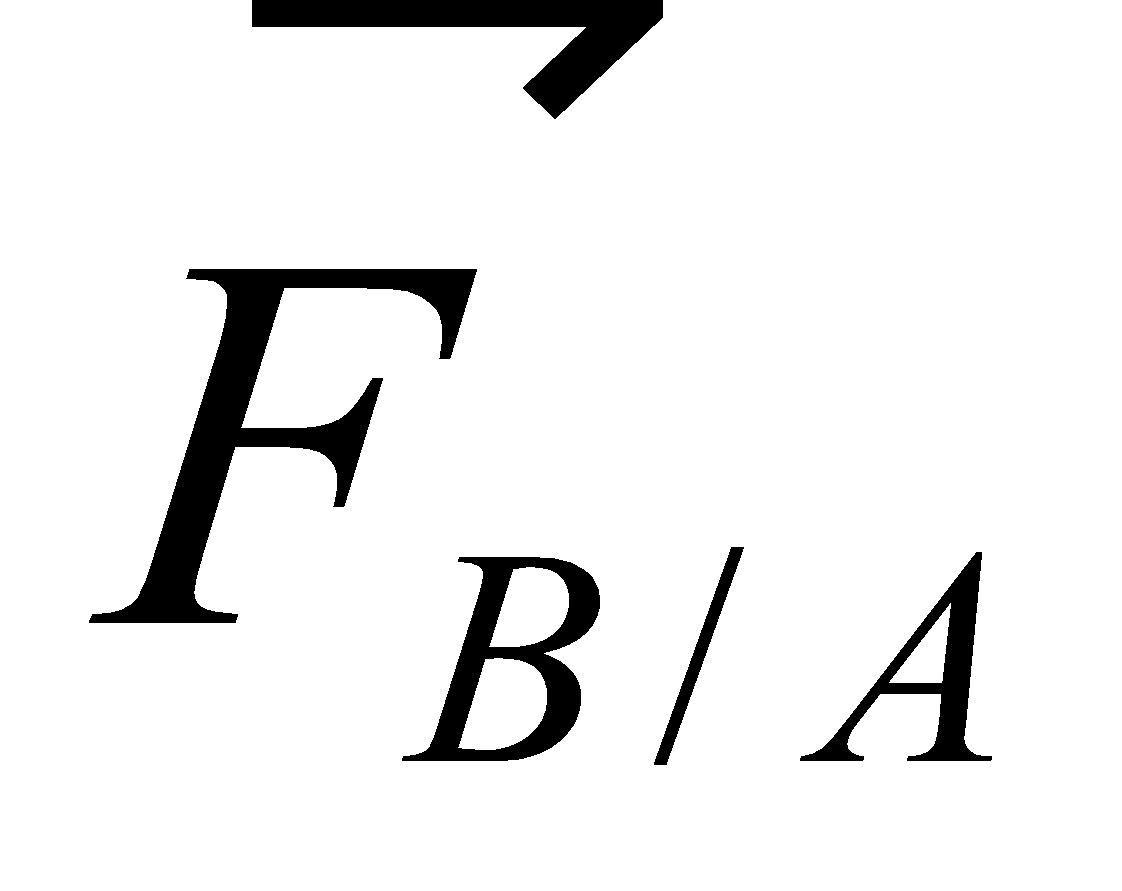(réaction) de même droite d’action, mais de sens opposé.

Vectoriellement, on écrit : .

On dit que les deux forces sont directement opposées.

Remarque : L’action et la réaction peuvent avoir des effets similaires ou totalement différents

III-2. Exemples d’illustration

On lance les boules (A) et (B) l’une vers l’autre. A leur rencontre elles s’exercent mutuellement les forces 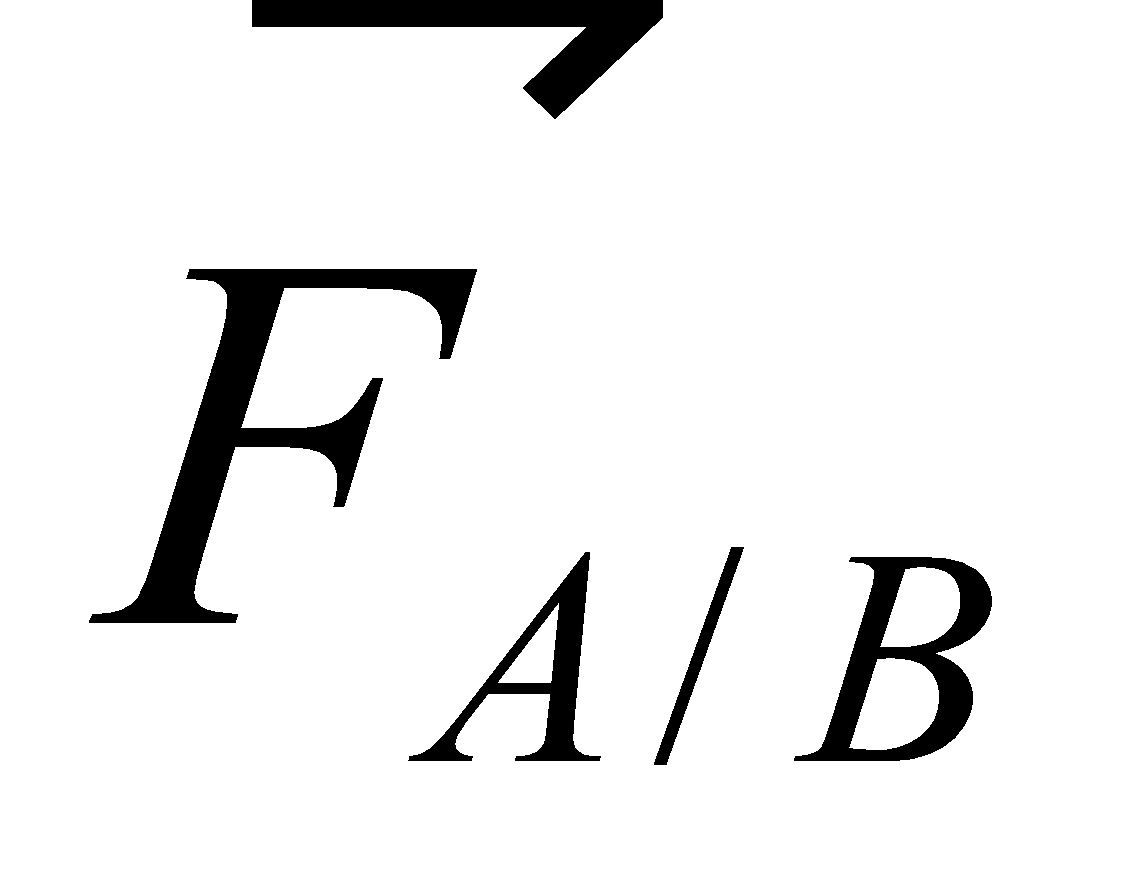et 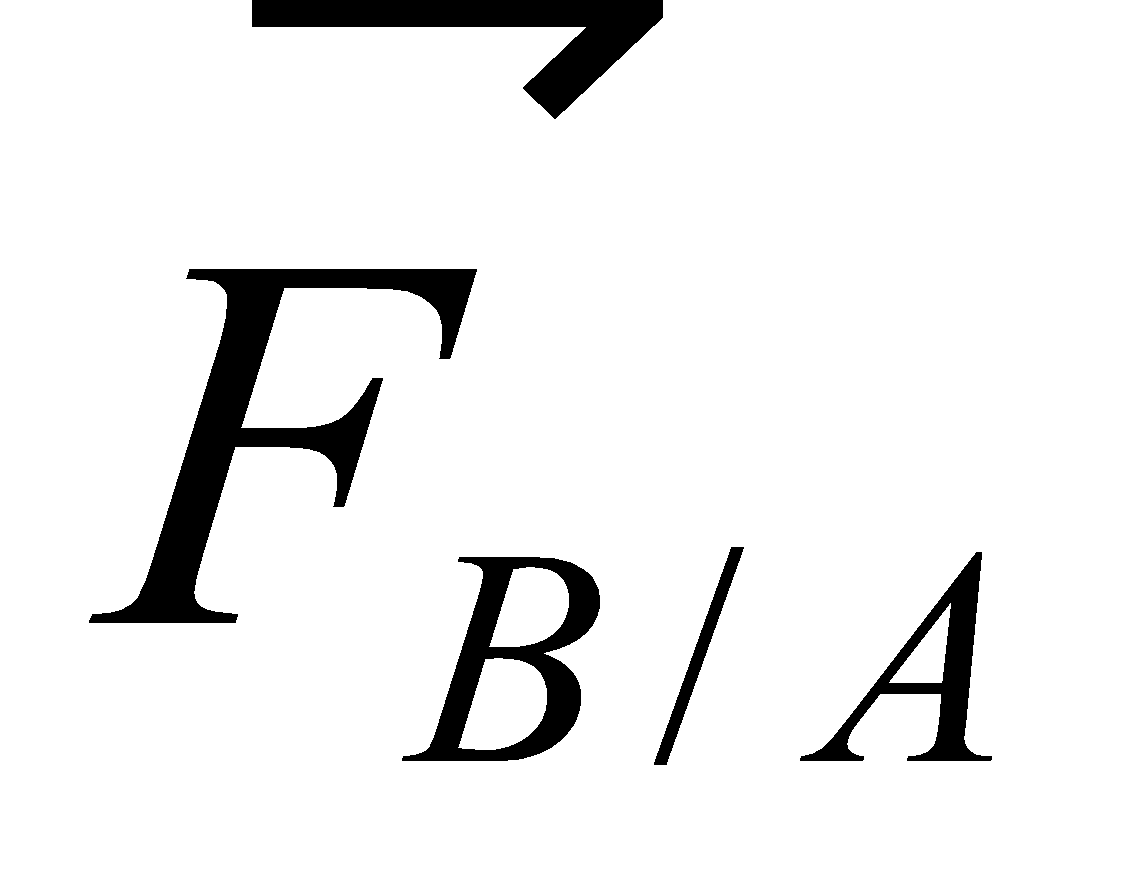directement opposée : .

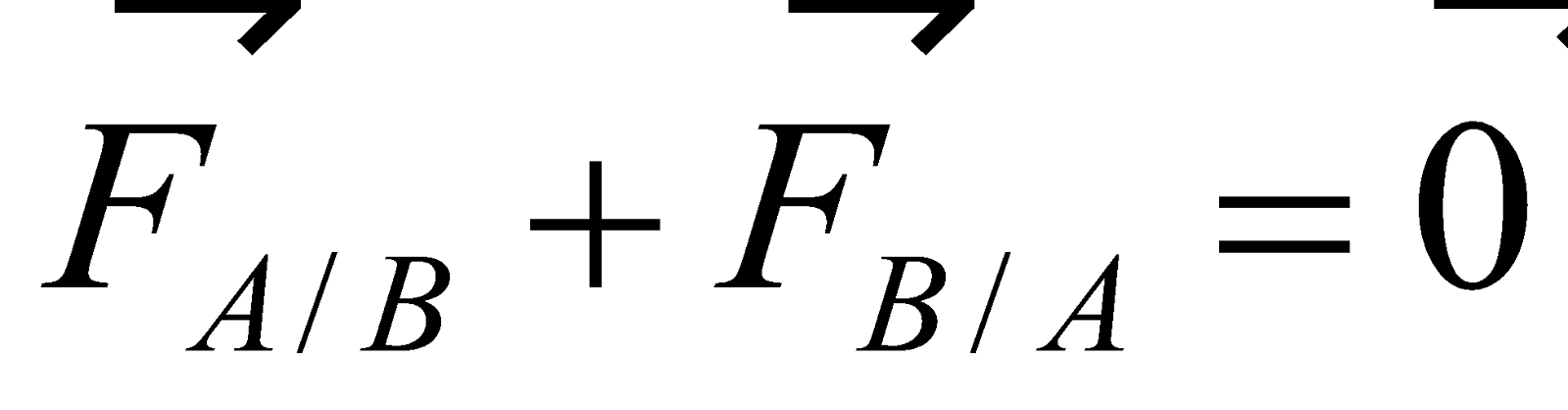Exemple 2

 

Les charriots C₁ et C₂ portent les aimants (A₁) et (A₂).

Lorsqu’on approche les charriots, les aimants s’attirent ou se repoussent  suivant les pôles en regard. Ils s’exercent les forces et telles que .

Exemple 3 : Le solide (S) exerce sur la table la force . La table exerce sur le solide la force (réaction du support) telle que .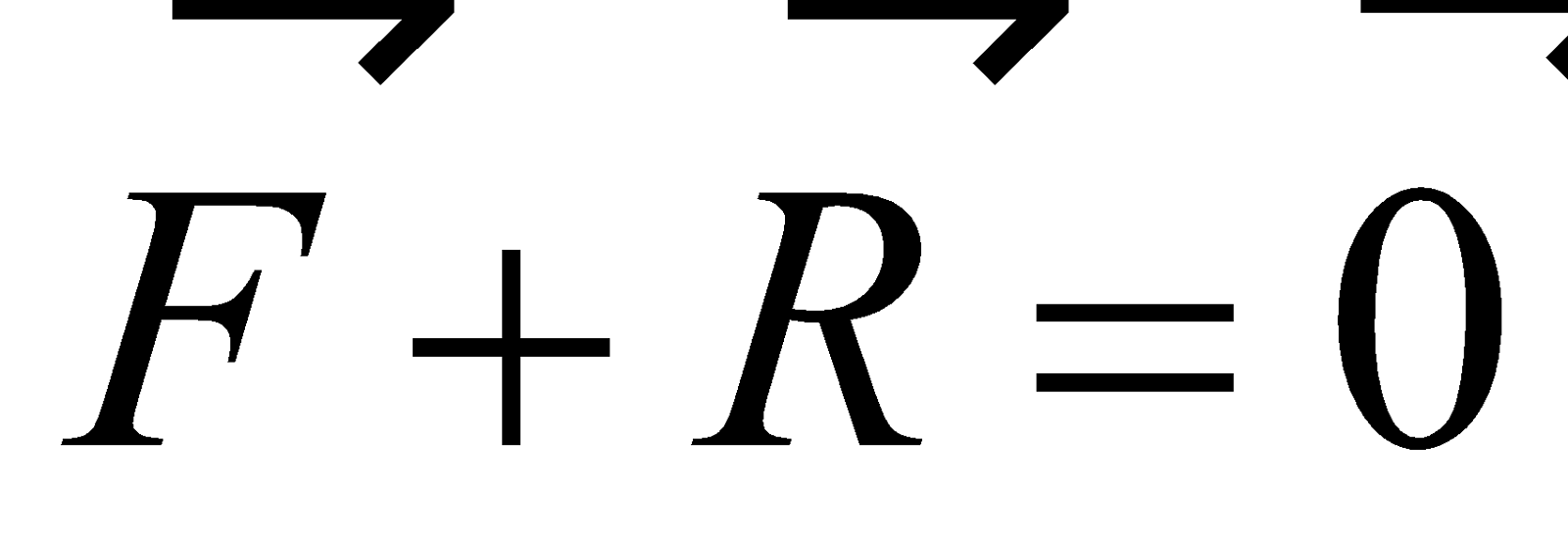

Exemple 4 : Le solide (S) agit sur le ressort en le déformant (force ), le ressort agit sur le solide en l’empêchant de tomber (force  : tension du ressort).

Exercice d’application

Deux boules sphériques sont placées dans un récipient cylindrique.

Faire l’inventaire des forces appliquées à chacune des boules           

Solution

Faisons l’inventaire des forces appliquées à chacune des boules :

• Poids de la boule b1
• Poids de la boule b2
• Réactions 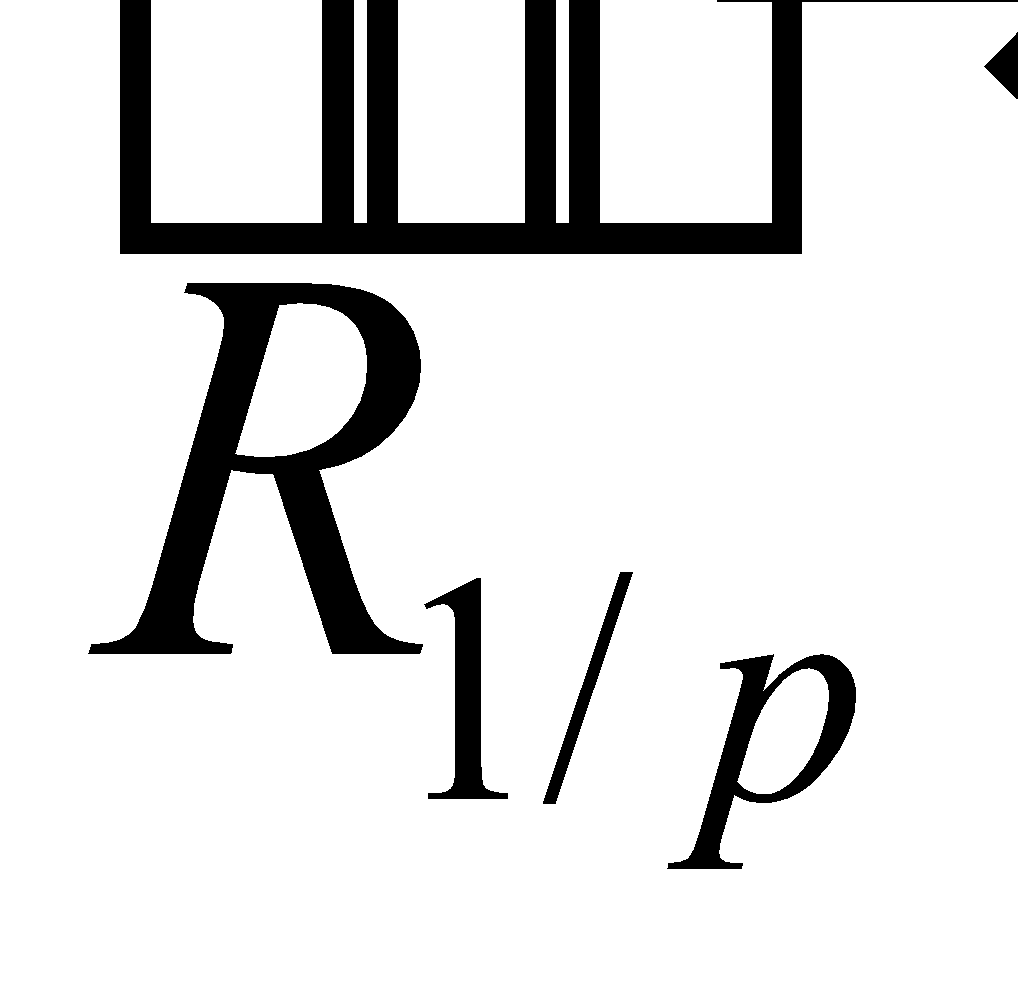et des  boules b1 et b2 sur le récipien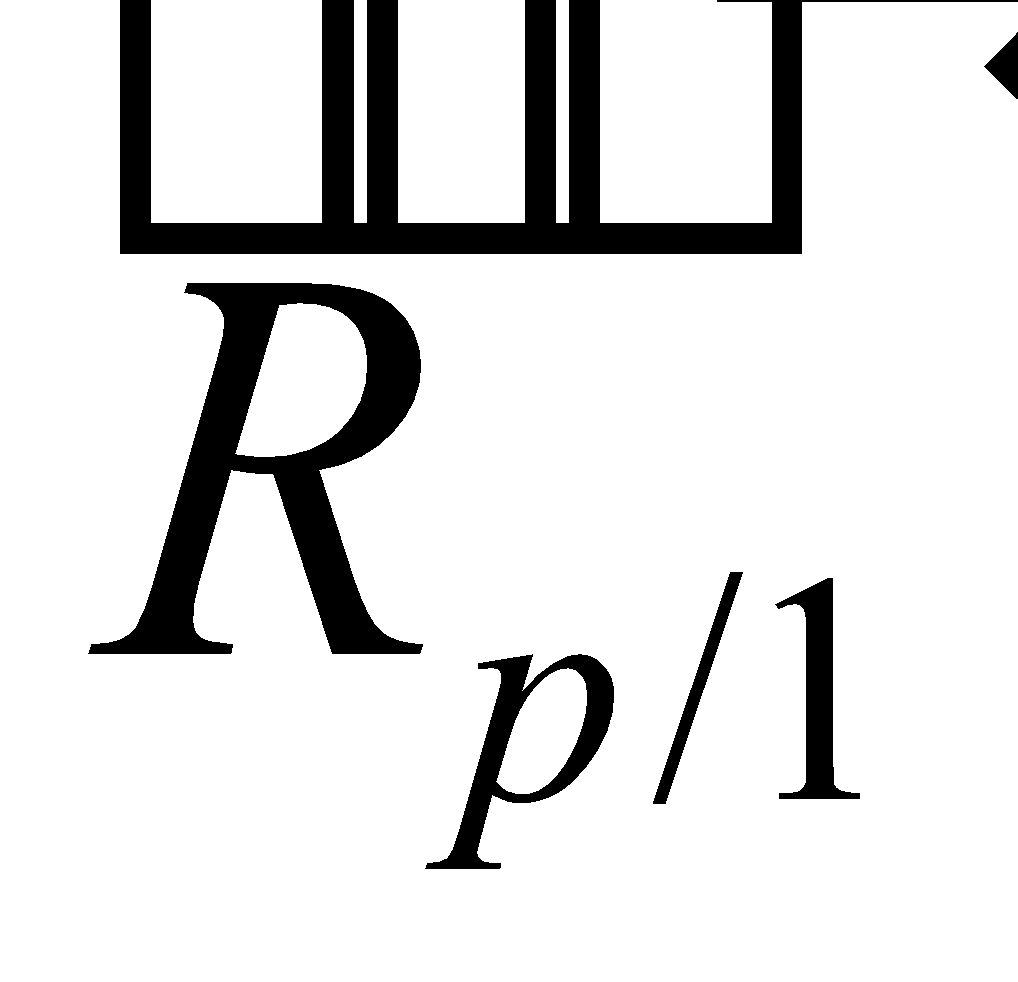t , et 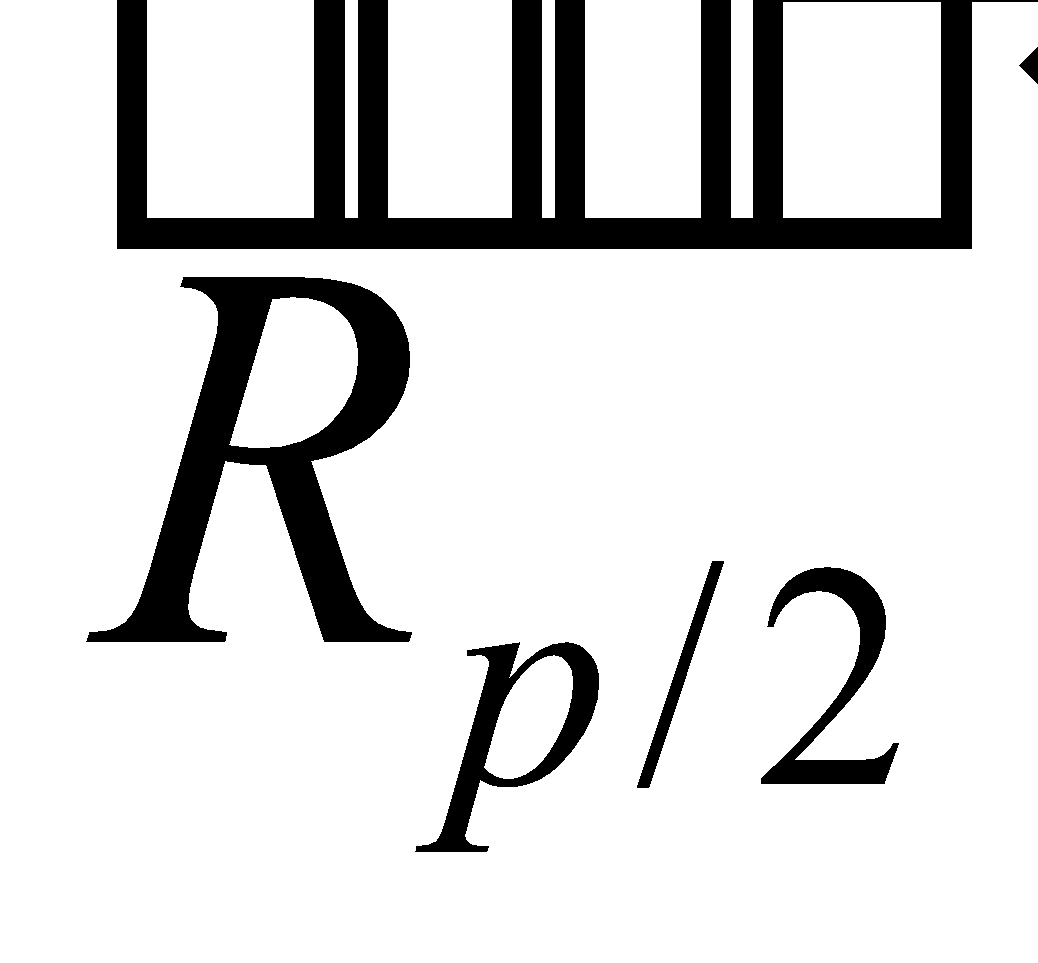du récipient respectivement sur les boules 1 et 2.
• Réactions 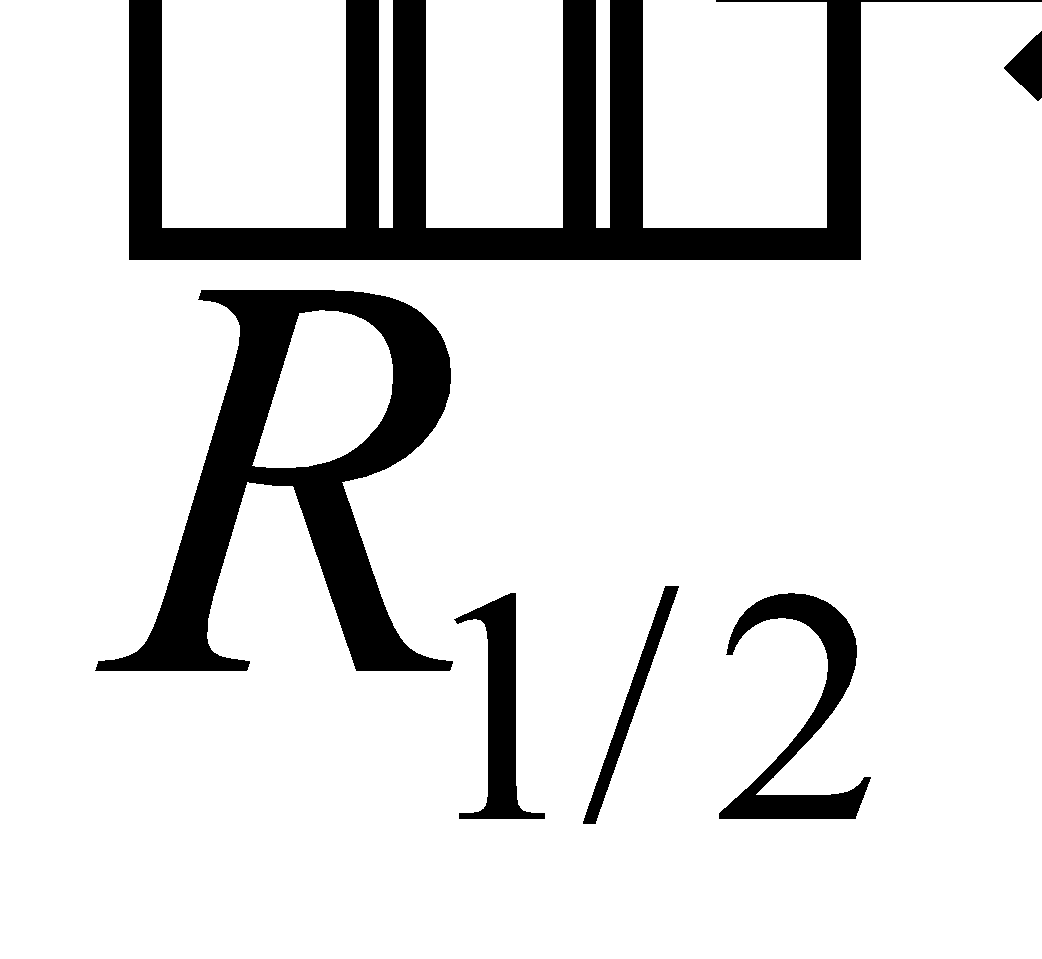et 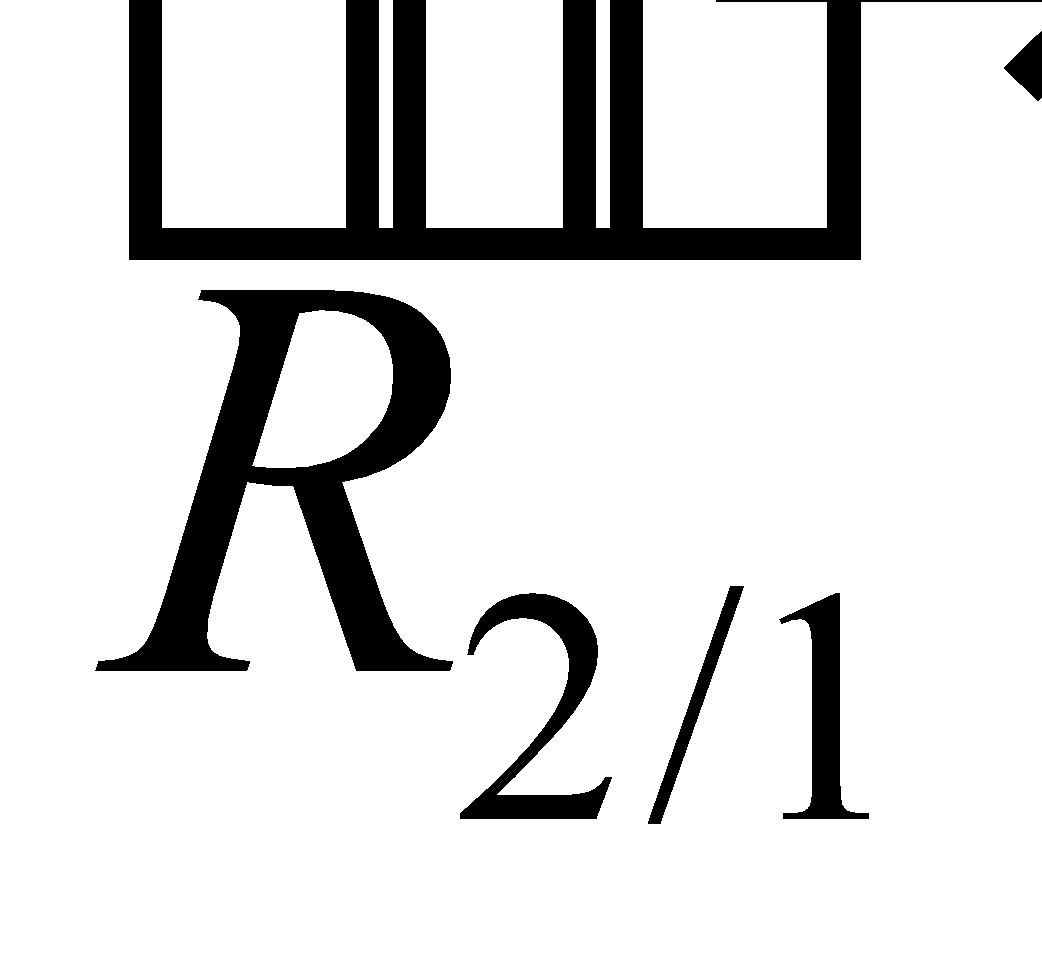respectives de la boule 1 sur 2 et de la boule 2 sur 1

4. METHODOLOGIE D’ETUDE D’UN SYSTEME

Pour étudier un système, il faut identifier :

• Identifier clairement le système à étudier ;
• Faire le bilan (inventaire) de toutes les forces qui s’exercent sur le système ;

Remarque : Les forces de distances peuvent être : le poids (force de pesanteur), la force magnétique, et la force électrostatique.

Application

Lors de la fête des sciences au lycée, un panneau porte le message suivant : vive la physique. Ce panneau repose sur un support et soutenue sur sa partie supérieur par des fils . Voir figure.

1. Faire l’inventaire de toutes les forces appliquées au panneau
2. Représenter ces forces sans tenir compte d’une échelle
3. Classer ces forces (en forces localisées et en forces réparties)
4. On considère le système ( panneau + support), identifier les forces intérieures et extérieures au système

Solution

1. Inventaire des forces

Système panneau

Forces de contact

• Tension du fil 1
• Tension du fil 2
• Réaction du support

Forces à distances

• Poids

2. Voir figure 
3. Classons les forces

Forces  réparties : et

Forces localisées : et

4. Forces intérieures : , Forces extérieures : , , ,

V. EVALUATION

Exercice 

On exerce sur un solide, des forces F₁ et F₂ orthogonales dont les droites d'action se coupent en un point B. Déterminer graphiquement puis par le calcul, la force F  = F₁  +  F₂.    A.N F₁= 10N; F₂= 20N. Quel est l'angle que fait la direction de F avec celle de F₁?

Solution

1)

2) = (+)=F₁² + F₂² + 2

                              =10² + 20² =500

F= 22,36 N