Equilibre d’un solide soumis à des forces non parallèles

Equilibre d’un solide soumis à des forces non parallèles

Un solide est en équilibre ; dans un référentiel donné, lorsque tous ses points sont immobiles dans ce référentiel.

1. Equilibre d’un solide soumis à deux forces

I .1 Description et schéma du dispositif expérimental :

Un polystyrène de masse négligeable est fixé en A et B à deux dynamomètres  (D₁) et (D₂)  par l’intermédiaire de deux fils (f₁) et (f₂) de masses négligeables.

Aux points A et B les deux fils exercent sur le polystyrène deux forces de tractions F₁ et F₂ lorsque les dynamomètres sont sous tension.

                           On observe que :

-les deux  dynamomètres indiquent la même valeur  F1=F2=4.2N

-les deux fils sont sur la même droite

-le polystyrène est immobile : il est en équilibre.

                       I.2 Condition d’équilibre :

Etudions maintenant l’équilibre du polystyrène. Représentons les vecteurs forces F₁ et F₂  qui s’exercent sur le polystyrène à l’échelle : 1cm →1,0 N.  =

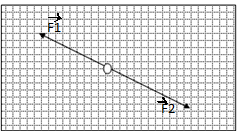
Nous notons que lorsque le polystyrène est en équilibre, les forces F₁ et  F₂ ont :

•  La même droite d’action
•  des sens contraires
•  La même intensité: F₁    =  F₂    

En  résumé on a : F1+F2 = 0  

I.3 Généralisation

Lorsqu’un solide soumis à deux forces extérieures F₁ et F₂ est en équilibre :

• Les deux forces ont la même droite d’action.
• La somme vectorielle de ces forces est nulle : F₁ + F2=0

Remarque

Cette condition d’équilibre est nécessaire mais pas suffisante. En effet dans l’exemple ci-contre F₁ et  F₂ n’ont pas la même droite d’action et  F₁+ F₂ = 0 , on obtient alors un couple de forces qui a pour effet de faire tourner le solide autour d’un axe (?)

 : ce dernier n’est pas en équilibre. 

        I.4 Applications :

• Méthodologie pour étudier l’équilibre d’un système :

Pour étudier l’équilibre d’un système il faut :

• Choisir un système d’étude : c’est-à-dire le solide dont on veut étudier l’équilibre.
• Faire le bilan de forces extérieures qui agissent sur le système
• Enoncer les conditions d’équilibres dont  Fexterieurs=0

On peut exploiter cette condition de deux manières :

• Par la méthode graphique 
• Par des projections sur des axes perpendiculaires convenablement choisis.  

        I.4.1 Equilibre d’un solide suspendu à un fil :

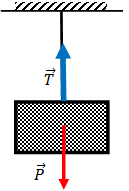
• Système étudié : le solide (S)
• Référentiel terrestre supposé galiléen                               
• Bilan des forces extérieures qui exercent sur (S)

• Son poids P
• La tension du fil

•  Condition d’équilibre

    P+ T =0    P = -T   

P=T=mg 

Remarque : La tension du fil est toujours portée par l’axe du fil et est dirigée du système d’étude vers le fil.

I.4.2 Equilibre d’un solide suspendu à un ressort :

• Système étudié : le solide (S)
• Référentiel terrestre supposé galiléen 
• Bilan des forces extérieures qui exercent sur (S)

•  P   le poids du solide  
• T     la tension du ressort

• Condition d’équilibre : 

    P+ T =0    P = ?T      P=T   or  P=mg  et

T=k(l – l0)

Finalement:   mg =k(l– l0)    

Où 

       K est appelé constante de raideur du ressort.

       ?₀ est la longueur à vide du ressort, 

       ? sa longueur à l’équilibre 

       ?l = ?-?₀  son allongement.

   I.4.3 Equilibre d’un solide sur un plan horizontal

•  Système étudié : le solide (S)
• Référentiel terrestre supposé galiléen 
• Bilan des forces extérieures qui exercent sur (S) :

• Son poids P  
• La réaction  R du plan sur (S) 

• Condition d’équilibre : 

  P et R ont la même droite d’action (voir schéma). 

  La droite d’action de la réaction R du plan passe par le centre de gravité du solide.

     P+ R=0     P=? R  ⇒   Finalement on a :   P=R=mg  

 II .Equilibre d’un solide soumis à trois forces non parallèles

      II.1  Description et schéma du Dispositif expérimental :

Un polystyrène de masse négligeable est fixé à trois dynamomètres (D₁), (D₂) et (D₃) par l’intermédiaire de trois fils de masses négligeables.

Les trois fils exercent sur le polystyrène trois forces de tractions F₁, F₂ et F₃  lorsque les dynamomètres sont sous tension.

On obtient le dispositif ci-dessous :

 On constate que :

• Les trois fils se situent dans un même plan et se rencontrent en un même point : ils sont coplanaires et concourants.
• Le polystyrène est immobile : il est en équilibre.

          II.2 Condition d’équilibre

Repérons sur une feuille placée sous le polystyrène les 3 fils, c'est-à-dire les droites d’action des trois forces T₁, T₂ et  T₃ qui s’exercent sur le polystyrène.

Les intensités de ces trois forces sont, quant à elles, indiquées par les dynamomètres. Nous constatons que les droites d’action des forces   T₁, T₂ et  T₃ sont concourantes en un point O.

• Représentons à l’échelle les trois forces : T₁, T₂ et  T₃ en O.

• Représentons la force F définie par  F=T1+ T2  

On constate que :

    F=?T3 or F=T1+ T2 T1+ T2=?T3 T1+ T2+T3=0    

    Finalement nous pouvons conclure que lorsque le polystyrène est en équilibre :

• les forces T_1, T2  et  T₃  Coplanaires et Concourantes
• leur somme vectorielle est nulle: T1+ T2+T3=0 

             II.3 Généralisation :

Lorsqu’un solide soumis à des  forces non parallèles est en équilibre :

Les  forces sont coplanaires et concourantes.

La somme vectorielle de ces forces est nulle 

II.4 Application : équilibre d’un solide suspendu à un ressort sur un plan incliné :

Considérons un solide (S) de masse m= 1000g  posé sur un plan incliné comme le montre la figure ci-contre. L’angle formé par le plan horizontal et le plan incliné est = 30°

Il n’a pas de frottements entre le plan incliné et le solide (S). celui-ci est maintenu en équilibre grâce à un ressort dont la raideur vaut k=200N/m lorsque le solide (S) est à l’équilibre, l’allongement du ressort vaut ?l=2,5cm.

a°)  Faire le bilan des forces qui s’exercent sur le solide (S)

b°)  Déterminer les intensités  de toutes les forces appliquées au solides (S).

   Résolution :

a°)  Système étudié : le solide (S)

référentiel terrestre supposé galiléen 

Bilan des forces appliquées au solide (S) :

• Son poids P 
• La tension T  du ressort 
• La réaction R du plan sur (S)

b°)  Déterminons les intensités  de toutes les forces appliquées au solides (S).

   P=mg= 1x10=10N    ;   T=kΔ? =2002,5.10^-2 =5N

Pour déterminer l’intensité de la réaction, on peut utiliser soit la méthode graphique, soit la méthode géométrique,  soit la méthode analytique.

• ETUDE GRAPHIQUE

Prenons pour échelle : 1cm2,0N

Ainsi : P=10N  102 =5cm        et    T=5,0N     5 2 = 2,5cm 

Translatons les vecteurs P , T  et R  et traçons les vecteurs  P et T  en respectant l’échelle. Après le tracé de R  on obtient :

La mesure de R correspond à 4,4cm ; cette valeur rapportée à l’échelle  donne : R=4,42=8,8N

• ETUDE ANALYTIQUE :

Choisissons deux axes de cordonnées (l’un passant par T   et l’autre passant par  R )

Condition d’équilibre : P +R+T=0    

Les composantes de P, R et T   suivant les axes (OX) et (OY) sont :

P{px=-Psin() Py= -Pcos()               T= {T x=T Ty=0                 R{Rx=0 Ry=R

La condition d’équilibre s’écrit alors :  –Psin()-Pcos()+T0+0R= 00

D’où le système de deux équation à deux inconnues :    {-Psin+T+0=0 -Pcos+0+R=0

On en tire :   T= P sin ()      et   R=Pcos ()       

AN :    P=10N  ,   R= 8,7N    et   T= 5N  EVALUATION

Exercice 1 :

Un ressort  d’axe vertical de constante de raideur k₌5.10³ N/m supporte  un objet  (S) de masse m=5kg.

1) Calculer le raccourcissement du ressort. Prendre g= 10N/kg

            2) Une surcharge de masse m’= 1kg est posée sur (S) .De combien varie  l   le ressort se raccourcit ?

Exercice 2 :

Un cube de côté a = 10cm et de masse m = 1,5 kg repose sur un plan très rugueux. Il existe donc d’importants frottements entre le cube et le plan. Le plan est incliné d’un angle α = 30°. Le solide reste immobile.

1. Représenter  les forces  qui s’exercent sur le solide. 
2. Déterminer et représenter la réaction du plan sur le solide à l’équilibre.
3. En déduire la valeur des frottements exercés sur le solide.

Solution :

Exercice 1 :

1. Le raccourcissement du ressort :

Système étudié : objet  (S)

Référentiel terrestre supposé galiléen                                   

Bilan des forces appliquées à l’objet (S) :                                                   

• Son poids P 
• La tension T  du ressort 
• Condition d’équilibre : 

    P+ T =0    P = ?T      P=T   or  P=mg  et T=kΔ?

Finalement:            mg =k l       l=mgk             

A.N :   l =5105.10³        l= 10^-2 m = 1 cm

2) Le nouvel raccourcissement du ressort :

• Condition d’équilibre : 

    P'+ T =0    P' = ?T      P'=T   or  P'=m'g  et T=kΔ?’

Finalement:            m'g =k l       l'=m'gk           

A.N :   l =1105.10³           l= 5.10^-2 m = 5 cm 

Exercice 2 :

1. Représentons  les forces  qui s’exercent sur le cube  

Système étudié : le solide

Référentiel terrestre supposé galiléen 

Bilan des forces appliquées au solide :

• Son poids P 
• La réaction  R du plan sur (S)  et f la force de frottement

2. Déterminons la réaction  R  du plan sur le solide à l’équilibre

Condition d’équilibre : P +R+f=0

Les composantes de P, R et f   suivant les axes (OX) et (OY) sont :

P{px=-Psin(α) Py= -Pcos(α)               f= {f x=f fy=0                 R{Rx=0 Ry=R       {-Psin+f+0=0 -Pcos+0+R=0

R = Pcos()         A.N: R = 1,5×10× cos 30       R=12,99 N

2) La valeur des frottements exercés sur le solide

  f= Psin()   A.N:    f= 1,5×10×sin30         f= 7,5 N